Los modelos de resolución de circuitos con diodos más usados son 4:
Modelo exacto
1ª Aproximación
2ª Aproximación
3ª Aproximación
Primeramente analizaremos la resolución de forma exacta y en el siguiente apartado se verán los tres tipos de aproximaciones. Modelo Exacto El circuito que queremos resolver es el siguiente. Primeramente y mirando la temperatura en la que estamos trabajando tomamos del catálogo los siguientes valores para Tª = 27 ºC (temperatura ambiente): Con esto podremos continuar calculando: De la ecuación exacta del diodo: Tenemos 2 incógnitas y una ecuación, necesitamos otra ecuación que será la ecuación de la malla: Y ahora tenemos 2 incógnitas y 2 ecuaciones, resolvemos:
Nos queda que es imposible despejar la V, es una "ecuación trascendente". Para resolver este tipo de ecuaciones hay que usar otro tipo de métodos, aquí lo resolveremos por "tanteo", que consiste en ir dándole valores a una de las incógnitas hasta que los valores se igualen. En este ejemplo hemos usado una malla, pero si tuviéramos más diodos, tendríamos más exponenciales, más mallas, etc... Esto es muy largo, por eso no se usa (a no ser que dispongamos de un ordenador y un programa matemático para resolver este tipo de ecuaciones).
Para poder hacerlo a mano, vamos a basarnos en unos modelos aproximados más o menos equivalentes del diodo. Estos modelos equivalentes aproximados son lineales, al ser aproximados cometeremos errores.
Existen tres aproximaciones muy usadas para los diodos de silicio, y cada una de ellas es útil en ciertas condiciones.
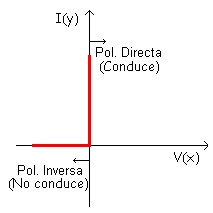
1ª Aproximación (el diodo ideal)La exponencial se aproxima a una vertical y una horizontal que pasan por el origen de coordenadas. Este diodo ideal no existe en la realidad, no se puede fabricar por eso es ideal.
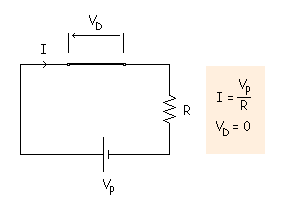
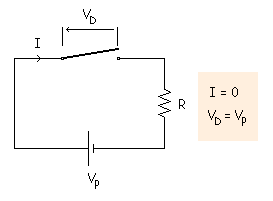
EJEMPLO:
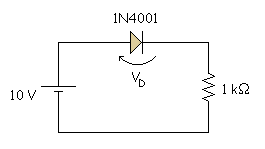
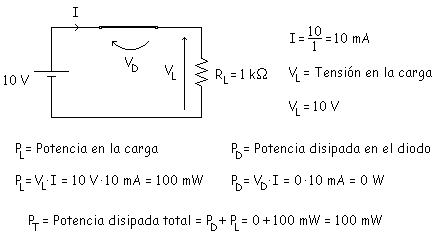
La exponencial se aproxima a una vertical y a una horizontal que pasan por 0,7 V (este valor es el valor de la tensión umbral para el silicio, porque suponemos que el diodo es de silicio, si fuera de germanio se tomaría el valor de 0,2 V).
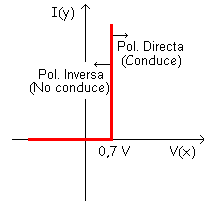
Polarización directa: La vertical es equivalente a una pila de 0,7 V.
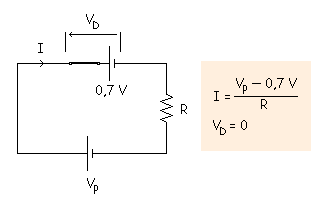
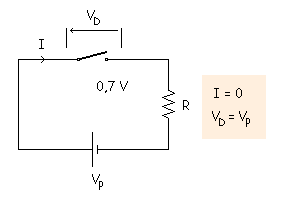
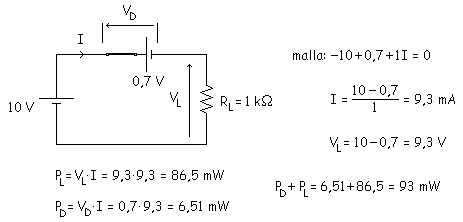
3ª Aproximación
La curva del diodo se aproxima a una recta que pasa por 0,7 V y tiene una pendiente cuyo valor es la inversa de la resistencia interna.
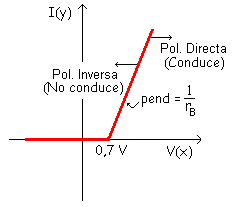
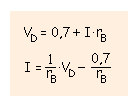
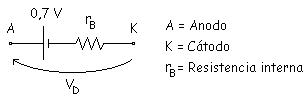
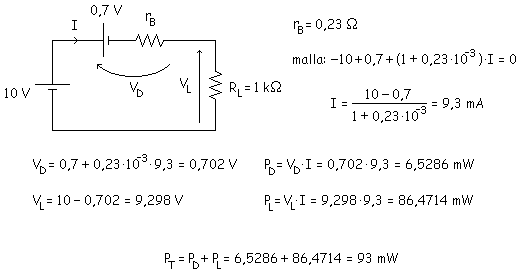
Como elegir una aproximación
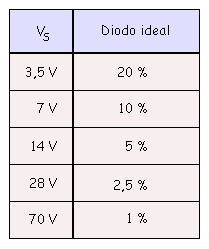
Para elegir que aproximación se va a usar se tiene que tener en cuenta, por ejemplo, si son aceptables los errores grandes, ya que si la respuesta es afirmativa se podría usar la primera aproximación. Por el contrario, si el circuito contiene resistencias de precisión de una tolerancia de 1 por 100, puede ser necesario utilizar la tercera aproximación. Pero en la mayoría de los casos la segunda aproximación será la mejor opción.
La ecuación que utilizaremos para saber que aproximación se debe utilizar es esta:
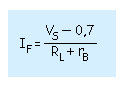






No response to “Los modelos de resolución de circuitos”
Publicar un comentario