Observando la
figura #21 se puede calcular el área del pulso con base igual a “e“ y altura “h” igual a k/e obteniéndose como resultado el área igual a k, la cual se
mantiene constante para los tres rectángulos.
Se observa que
si la base “e“ disminuye la altura “h” aumenta mientras el área se mantiene
constante.
En el limite
cuando “e“ tiende a cero se tiene:
Con este procedimiento se ha podido demostrar como obtener
una función, que tiene una altura infinita, un ancho infinitesimal y un área
finita.
La figura #22
muestra la representación gráfica de la función impulso unitario.
Se puede
observar que la función impulso existe en aquellos instantes en los cuales se
anula su argumento. Con esta consideración, si el argumento de la función delta
es una función p(t), entonces la función delta existirá en todos aquellos
valores en los cuales se anule p(t).
Figura #22
Representación gráfica de
la función impulso.
La función
impulso es factible de ser desplazada en el eje horizontal, así como también
escalada en magnitud, el procedimiento es similar al procedimiento ya descrito
para las funciones anteriores. La figura # 23 muestra la función impulso
desplazada y escalada en magnitud.




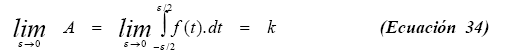



No response to “Función impulso unitario. II”
Publicar un comentario