Función impulso unitario.I

Función impulso unitario.

Esta función tiene la propiedad mostrada por la siguiente integral:

                                   

para cualquier f(t) continua en t = t₀ , con t₀ finito.

La función, según la ecuación (33), selecciona o separa el valor particular de f(t) para t = t₀ durante el proceso de integración, por esta razón, se designa a esta propiedad como propiedad de muestreo de la función impulso.

Veamos dos ejemplos que facilitan la comprensión de este hecho.

i) Evaluar la integral definida:

              

Solución: aplicando la ecuación (33) y tomando t₀ = p, se tiene:

                       

Observe que se ha tomado:    f(t) = e^{cos t}   y  se evalúo en t₀ = p .

ii) Evaluar:

        

Solución: Analizando la integral observamos que x₀ = 0, no aparece explícitamente, pero podemos considerar lo siguiente:

      

Como x₀ = 0 no está entre el intervalo 1 < x < ¥, el resultado de la integral es cero.

Esto es:

        

Ejercicio propuesto:

Evaluar la integral:               

La ecuación (33) muestra que la funcion impulso no es una función ordinaria. Sin embargo, d(t) se puede tratar como una función que obedece formalmente las reglas de integración, si basamos las conclusiones en la ecuación (33) y no en las propiedades puntuales de d(t).

La función impulso puede ser definida como una función pulso, la cual tiene una amplitud infinitamente grande y un ancho infinitamente pequeño y cuya área es finita e igual a la unidad.

La función impulso también es conocida como función delta o función de Dirac.

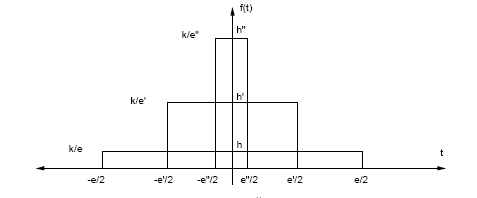
Una interpretación gráfica de la función impulso se puede obtener por medio de la figura # 21.

Figura #21

Interpretación gráfica de la función impulso.