La simetría que una forma de onda tiene respecto al eje “y” o al
origen, se puede determinar en forma analítica cambiando en la ecuación de la
forma de onda la variable “ t ” por “ - t ” y en dependencia del resultado
podemos determinar si la función es simétrica respecto al eje “y” o si no lo
es.
A continuación se dan los procedimientos necesarios.
a)
Funciones pares.
Se dice que una función es par si satisface la condición de que
(Ecuación
5)
De la ecuación # 5 se concluye que una función par es simétrica
respecto al eje vertical en el origen.
La figura # 2 muestra la gráfica de una función par. Observe que
la misma es simétrica respecto a el eje vertical en el origen.
b)
Funciones impares.
Se dice que una función es impar si satisface la condición de que
(Ecuación
6)
De la ecuación # 6 se concluye que una función impar es
antisimétrica respecto al eje vertical en el origen.
Figura #2
Ejemplo de una función
par
La figura # 3 muestra la gráfica de una función impar. Observe que
la misma es simétrica respecto al origen.
Figura #3
Ejemplo de una función
impar





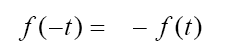



No response to “Funciones pares e impares.”
Publicar un comentario