Según se pudo
observar en la definición de la convolución, se debe hallar el producto
integral de las dos funciones desde -¥ hasta +¥. Por
esta razón, es necesario que se establezca un procedimiento que permita hallar
la convolución de dos funciones gráficamente, dejando una de ellas fija e ir
desplazando la otra a lo largo del eje horizontal desde -¥ hasta
+¥.
A continuación
se procederá a dar un procedimiento para hallar la solución de la convolución
de dos funciones cuyas gráficas son continuas por intervalos.
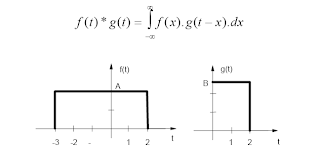
Supongamos que
se desea hallar la convolución de dos funciones f(t) y g(t) cuyas gráficas
están dadas en la figura #27 . Como se puede observar las dos funciones están
constituidas por pulsos rectangulares de duración dada.
Para hallar la
solución de este problemas, enumeramos varios pasos para facilitar su
comprensión.
PASO #1
Aplicar la
definición de la convolución dada por la ecuación (46), esto es, para las
funciones dadas:
Figura #27
Representación gráfica de
la funciones f(t) y g(t)
las cuales se van a
convolucionar.
PASO #2:
Según el
integrando de la ecuación del paso #1, se debe realizar un cambio de variable.
Se obtienen f(x) y g(x). Se cambian
directamente las variables en las ecuaciones de cada una de las funciones,
obteniéndose las gráficas de la figura # 28, en la cual se ha cambiado la
variable “t” por “x”.
Figura #28
Representación gráfica de
la funciones f(x) y g(x)
(cambio de la variable
“t” por “x”)
PASO #3:
Dado que una
de las gráficas debe ser desplazada y la otra mantenerse fija, establecemos que
la función a ser desplazada es la g(x).
Bajo esta consideración se halla la transpuesta de la función g(x), lo cual se obtiene cambiando “ x”
por “ - x ” .
En la gráfica
de la figura #29 se muestra la función transpuesta de g(x) .
PASO #4:
Dar un
desplazamiento genérico “t “ a la función g(-x), con lo cual se obtiene la función g(t-x). La representación de la función g(t-x) se muestra en la
figura #30. Observe en la gráfica de g(t-x), que se ha dado un desplazamiento
“t” y se ha denotado el lado derecho del pulso rectangular con la letra “ t ” y
el izquierdo como “ t - 2 ”.
Figura #29
Gráfica de la funciones
f(x) y g(-x)
Esta letra
representa la variable “t” que tomará
distintos valores entre -¥ y +¥. Al darle valores a “t”,
lo que se está haciendo es desplazar la gráfica de g(t-x) en el eje “t”.
Los valores que se dan a “t” corresponden a intervalos bien definidos y que
pueden ser determinados de una manera muy sencilla. Si la gráfica de g(t-x)
está totalmente a la izquierda de f(x) ( esto es, t £ -3), el producto integral es cero. Si el lado derecho de g(t-x)
penetra por el lado izquierdo de f(x) de manera que se solapen ( t > -3) el
producto integral será diferente de cero mientras se mantenga dentro del
rectángulo de la gráfica de f(x) (esto es, el producto integral será diferente
de cero siempre que
Figura #30
Desplazamiento de la
gráfica de la función g(t-x)
halla
solapamiento entre las dos gráficas) y hasta que el lado t-2 haya salido por el
lado derecho de la gráfica de f(x). Una vez que el lado denotado como t-2 de
g(t-x) supera el lado derecho de la gráfica de f(x), el producto integral se
hace igual a cero.
En los pasos
sucesivos se realiza un análisis para cada uno de los intervalos.
PASO #5:
Intervalo t<-3.
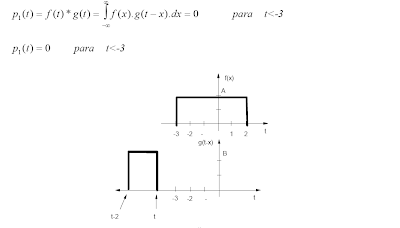
Consideremos
que la gráfica de g(t-x) se encuentra ubicada según la figura #31, esto es,
para valores de t < -3 ( observe que la variable “t” está asociada con el
lado derecho de la gráfica g(t-x) y es la que nos permite hacer el estudio para
los diferentes intervalos).
Bajo la
consideración anterior, el producto integral es cero, debido a que f(x) vale
cero para t < -3, esto se puede escribir:
Figura #31
Gráfica de la funciones
f(x) y g(t-x)
para un desplazamiento de
t<-3
PASO #6:
Intervalo -3 £ t<-1.
El análisis
para este intervalo es, según se muestra en la figura # 32. Observe que ahora
el valor de “t” se encuentra definido como -3 £
t < -1.
El valor de la
convolución para este intervalo es
Observe que los límites de la integral
corresponden al área común para ambas gráficas de las funciones.
El valor de la convolución para este
intervalo es:
PASO #7:
Intervalo -1 £ t<2.
Este intervalo
se pudo obviar si se consideraba todo el intervalo en que se solapan las dos
gráficas, es decir desde -3 hasta 2, ya que en este intervalo el
rectángulo de la gráfica de g(t-x) se encuentra dentro de la
gráfica de f(x). Sin embargo, para
facilitar la división del trabajo por intervalos, fue considerado.
En este caso
la gráfica de g(t-x) se desplaza con
valores de “t” en -1 £ t<2. En la figura #
33 se muestran las gráficas de f(t) y g(t-x).
Figura #32
Gráfica de la funciones
f(x) y g(t-x)
para un desplazamiento de
-3 £
t <-1
El cálculo de
la convolución está dado por:
Figura #33
Gráfica de la funciones
f(x) y g(t-x)
para un desplazamiento de
-1 £
t <2
PASO #8:
Intervalo 2 £
t < 4.
Para este
intervalo el lado derecho de la gráfica de g(t-x) está a la derecha del
rectángulo de la gráfica de f(x), es decir el rectángulo de g(t-x) va saliendo
del rectángulo de f(x).
Esta situación
se muestra en la figura # 34.
Figura #34
Gráfica de la funciones
f(x) y g(t-x)
para un desplazamiento
de 2 £ t < 4
PASO #9:
Intervalo t ³ 4.
Para este
intervalo el lado izquierdo de la gráfica de g(t-x) está a la derecha del
rectángulo de la gráfica de f(x), es decir el rectángulo de g(t-x) ha salido
totalmente del rectángulo de f(x). Ya que las gráficas no se solapan, el
producto integral o convolución es igual a cero.
Esta situación
se muestra en la figura # 35.
p4(t)
= 0 para t > 4
PASO #9:
La solución
total del problema se halla por medio de la suma de todos los productos
integrales parciales encontrados para cada uno de los intervalos. Considerando
esto, la solución está dada por:
p1(t) = 0 t
< -3
p2(t) = A.B.( t + 3 ) -3 £ t £ -1
p3(t) = 2.A.B -1 £ t £
2
p4(t) = A.B.( 4 - t )
2 £ t £ 4
p5(t) = 0 t
> 4
Figura #35
Gráfica de la funciones
f(x) y g(t-x)
para un desplazamiento de t
> 4.
Debe
observarse que los resultados son funciones de la variable “t”, lo cual permite
graficar en el tiempo el resultado de la convolución de las gráficas de f(t) y
g(t).
La gráfica de
todos estos productos parciales se muestra en la figura # 36.
Figura #36
Gráfica de la función p(t)
Ejercicio
propuesto: hallar la convolución de la funciones f1(t) y f2(t) cuyas gráficas
se muestran en la figura #37.
Figura
#37
Gráficas
de las funciones f1(t) y f2(t)
correspondientes
al ejercicio propuesto















No response to “Producto integral de funciones con soluciones gráficas.”
Publicar un comentario