A continuación
abordaremos un procedimiento matemático que aporta una manera diferente de
expresar una función f(t). Además este procedimiento permite realizar análisis
de formas de ondas, ya no en el dominio del tiempo, sino en el dominio de la
frecuencia, esto es, la nueva variable a
utilizar es “w” conocida como la frecuencia angular.
Sea la función
f(t) una función periódica de período T, la cual puede ser representada por la
serie trigonométrica
La ecuación 11 puede ser reescrita
utilizando el símbolo de sumatoria como sigue
(Ecuación 12)
siendo w0
= 2.p. f = 2.p.
/ T.
La serie de la
ecuación # 12 se denomina serie trigonométrica de Fourier.
El termino a0, independiente de la frecuencia, representa el
valor medio de f(t) en el tiempo.
Los valores
de a0,
an y bn se determinan por las ecuaciones siguientes:
(Ecuación
13)
(Ecuación 14)
(Ecuación 15)
Se debe
aclarar que no es necesario que el intervalo de integración sea simétrico
respecto del origen. El único requisito es que la integral se tome sobre un
período completo.




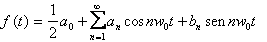




No response to “Series de Fourier”
Publicar un comentario