Desplazamiento
o traslación en el tiempo de una función.
El inicio y
fin de una función puede ser trasladado en el eje de los tiempos. Es así como
se produce el desplazamiento de la función, lo cual, no es más que un
corrimiento de la función en el eje horizontal.
Desde el punto
de vista matemático, esto no es más que sustituir la variable t en la ecuación
de la función por (a + t ),
donde “a” es una constante que puede tomar valores positivos o negativos.
Si los valores que toma la constante “a”
son positivos, el desplazamiento de la función es hacia la izquierda. Si “a” toma valores negativos el
desplazamiento es hacia la derecha.
Consideremos
la función definida como:
(Ecuación 7 )
El
desplazamiento de la función f(t) se hace sustituyendo en las ecuaciones que
definen la función a la variable “t” por “ t + a ”, donde “a”
representa el valor del desplazamiento que se desea dar a la función y su signo
el sentido: derecha o izquierda.
(Ecuación 8 )
Si sustituimos
la variable “t” por ( t + a ) con a = - 2 en la ecuación anterior nos
queda:
(Ecuación 9 )
Resolviendo
tenemos:
(Ecuación
( 10 )
Este resultado se muestra en la figura #
9-b.
Si se considera a = 2 se obtiene el resultado de la figura # 9-c.
Figura #9
Desplazamiento en tiempo de
una señal.






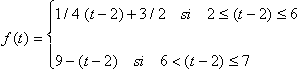



No response to “ ”
Publicar un comentario