El
escalamiento en tiempo de una señal, modifica la duración de la misma en
dependencia del valor de una constante
por la cual se multiplica el tiempo. Dicho de otra manera, el escalamiento en
tiempo de una señal se produce cambiando la variable “t” por “a.t” en la ecuación de la señal, donde “a” es una constante positiva. En el caso
de que a > 1, se produce una
compresión de la señal. En caso de que 0 < a < 1, se produce una expansión de la señal.
Consideremos nuevamente la función:
f(t) = A.sen(wt + j) (Ecuación
5 )
Si sustituimos
la variable “t” por “a.t” y damos a “a” valores mayores que 1 y valores
menores que 1, podemos obtener escalamiento en tiempo, es decir:
f(t) = A.sen(w.(at) + j) (Ecuación
6 )
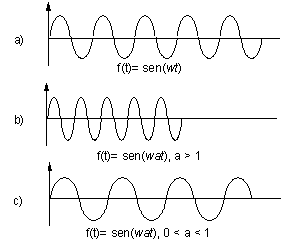
En la figura
#8 se muestra una señal senoidal, la cual ha sido escalada en tiempo. En la
parte a) la señal se muestra sin escalamiento. En b) la señal a sido escalada
en tiempo para valores de a > 1 ( se disminuye la duración de la señal)
mientras que para c) se escala en tiempo la señal para valores de 0 < a < 1 ( se aumenta la duración de la
señal)
Físicamente
hablando, podemos decir que al escalar en tiempo la señal senoidal anterior,
estamos variando la frecuencia de la señal, es decir, el número de ciclos por
unidad de tiempo de la misma. De esta manera, se puede entender porqué se
produce la compresión ( si a > 1 ) y la expansión ( si 0 < a < 1 ) de
la señal.
Figura #8
Escalamiento en tiempo de
una señal.





No response to “Escalamiento en tiempo de una función continua.”
Publicar un comentario